Software

Paper: OpenMolcas – a powerful electronic structure code going open-source

Felix

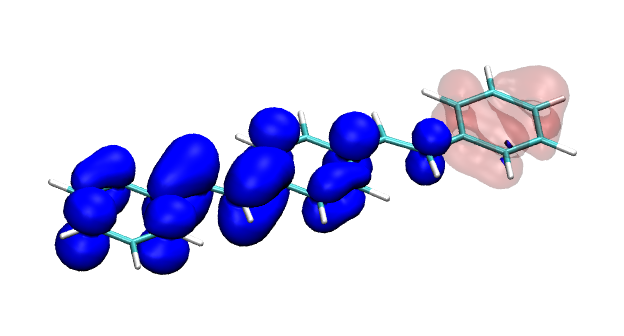
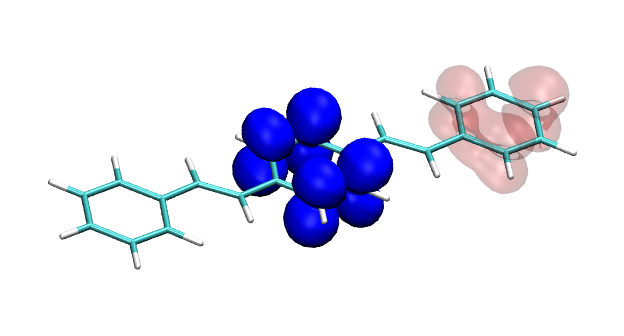
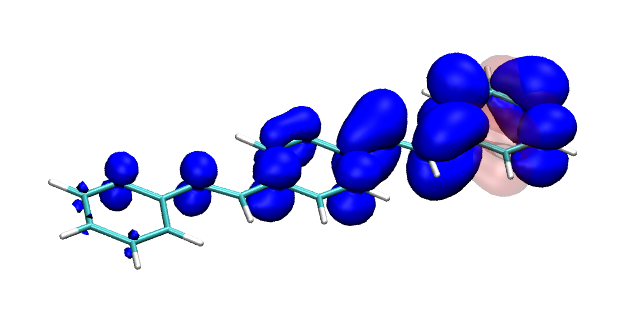
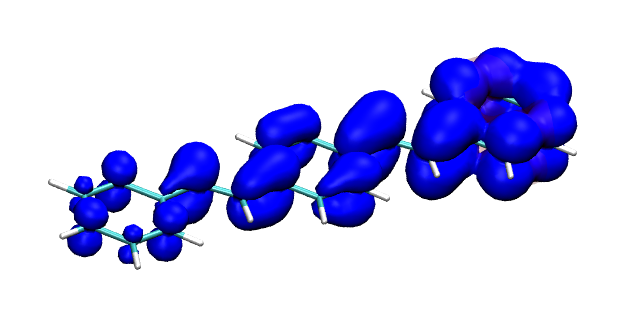
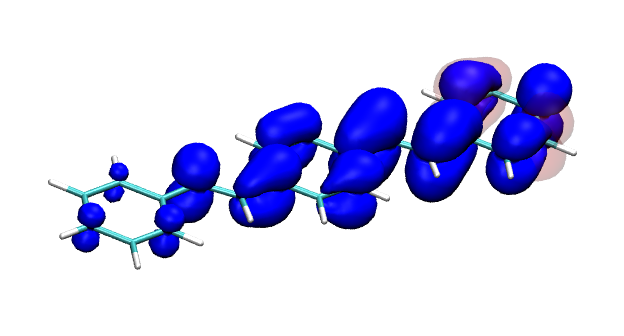
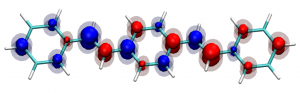
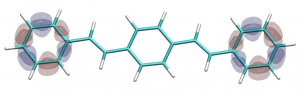
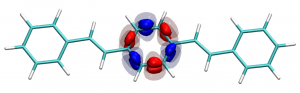
You can find the new paper describing the OpenMolcas package in JCTC – OpenMolcas: From source code to insight. OpenMolcas represents the open-source release of the previously commercially distributed Molcas package. Use OpenMolcas to gain access to powerful multireference methods for free and to have full control if you need to modify the source.

My own contributions to Molcas are concerned with the implementation of the wavefunction analysis module &WFA , as described in JCTC 13, 5343 (2017), and the interface to Columbus. Let me know if you have any questions about these.

New functionality for OpenMolcas

Felix

An update of the WFA module has been posted to OpenMolcas. This update integrates the fragment-based analysis that was previously only available via the TheoDORE code. In particular, it allows the automatic analysis of excited-state character in transition metal complexes [1, 2] with just a few added lines in the input file to OpenMolcas. This functionality is described here.

Thank you to Feng Chen from Loughborough University’s Research Software Engineering program for implementing the new code.

Release of TheoDORE 2.0 (beta)

Felix

Version 2.0 of the TheoDORE wavefunction analysis package has been released, download below. The two main features of TheoDORE 2.0 are the computation of conditional electron densities and compatibility with python3.

Conditional electron densities can be used for the visualisation of excited-state electron correlation, see ChemPhotoChem (2019). Below, the application of this method to a PPV oligomer is shown. Here, the probe hole (red) is always fixed on the terminal phenyl ring and the different shapes for the conditional electron density (blue) for the first six excited states is observed. One can see that for the different states the electron is either repelled, attracted or unaffected by the hole.

  • S1
  • S2
  • S3
  • S4
  • S5
  • S6

Continue reading →

Paper: Dynamics within an Exciton Model

Felix

Another paper working on improving the efficiency of surface hopping dynamics just appeared, this time in JCTC: “Surface hopping within an exciton picture – An electrostatic embedding scheme.” authored by M. F. S. J. Menger, F. Plasser, B. Mennucci, and L. González. In this paper, we explored the possibility of running nonadiabatic dynamics simulations within an exciton model. The main challenge in this endeavour was to derive a consistent energy expression for combining QM/MM electrostatic embedding calculations of the different chromophores.

Surface Hopping within an Exciton Scheme

To test the implementation, we ran simulations on a molecular dyad, where full TDDFT nonadiabatic dynamics simulations were available. Good agreement was found.

The method was implemented in the SHARC molecular dynamics package.

Paper: Vibronic coupling constants

Felix

You can find our new paper “Interstate vibronic coupling constants between electronic excited states for complex molecules” that recently appeared in JCP. The purpose of this paper was the development of a method that allows to determine interstate vibronic coupling constants, which are a decisive ingredient for model Hamiltonians used in quantum dynamics. Our idea was to start with a method based on wavefunction overlaps that is commonly used for trajectory dynamics simulations and adapt it for the case of quantum dynamics.